深度增强学习【1】走向通用人工智能之路
深度增强学习/深度强化学习的基本介绍以及对实现通用人工智能的探讨
现在但凡写人工智能的文章,必提Alpha Go。也正是因为Alpha Go在围棋人机大战中里程碑式的胜利,人工智能迎来了新的春天。 本文也不免俗套,从Alpha Go说起,但希望能指明一些被忽视的但对Alpha Go棋力有深远影响的技术。 围棋人工智能大致可以分为三个阶段1 :第一阶段以启发式算法为主,水平低于业余初段,代表软件即以静态势力函数为强项的手谈; 第二阶段以蒙特卡洛树搜索算法 为代表,水平最高达到业余5段,比如说 Zen ,Crazy Stone ;第三阶段以 深度学习 (Deep Learning)以及 增强学习 (Reinforcement Learning,也称强化学习)算法为突破,并战胜了人类职业九段棋手李世乭,这也就是Alpha Go的故事了。每每提到Alpha Go卓越的能力,往往归咎于深度学习的强大,但实际上增强学习算法也功不可没。这二者的结合被称之为 深度增强学习 (Deep Reinforcement Learning,DRL),最初见于DeepMind在Nature上发表的Human-level control through deep reinforcement learning。 本文试图从深度增强学习的角度来探讨通用人工智能的实现,并简要介绍了深度增强学习的基础知识、常见算法以及相关应用。
如何解决通用人工智能的难点
三座大山
创造出像你我一样具有自我意识和思考的人工智能估计是人世间最迷人的问题之一了吧,新的存在总是想窥探造物主的秘密。同 P=NP 问题一样,验证一个存在是否具有自我意识的难度(见图灵测试 以及 中文房间问题) 同创造一个具有自我意识的存在的难度究竟关系如何,恐怕可以看做是判断自我意识是否能涌现的关键了吧。本文不讲那么上层次的人工智能,先来谈谈 通用人工智能 。按照维基百科的解释,
强人工智能也指通用人工智能(artificial general intelligence,AGI),或具备执行一般智慧行为的能力。强人工智能通常把人工智能和意识、感性、知识和自觉等人类的特征互相连结。
本文所指的通用人工智能,便是可以处理通用任务的人工智能。 具体而言,我认为通用人工智能应包括以下三大特点或者说难点:
- 通用任务:既能唱歌绘画、又能下棋写诗,最重要的是要尽量减少对
领域知识(Domain Knowledge)的依赖。 - 学习能力:无论是通过逻辑推理的
演绎法来学习,或者是基于经验和记忆的归纳法来学习,都要通过学习来提高处理通用任务的适用性。 - 自省能力:也可以说是关于学习的学习,即
元认知,通过自省来纠偏行为。就像泰勒展开一样,我们大可以用低阶导数来逼近函数值,而无需考虑元认知的元认知这类高阶导数。
解决之道
David Silver(Alpha Go的第一作者)曾在ICML2016的Tutorial: Deep Reinforcement Learning讲到深度增强学习的前景
General Intelligence = Reinforcement Learning + Deep Learning = Deep Reinforcement Learning – David Silver
更进一步,『Reinforcement Learning defines the objective』(RL中有什么样的映射关系),『Deep Learning gives the mechanism』(DL如何学习给定的映射关系)。 我很同意深度增强学习便是解决通用人工智能难点的核心。 首先关于通用任务,几乎任何任务的解决都可以看做一个从形式编码的输入到决策分布输出的映射,而非线性的神经网络便是很好的 表征 (representation )学习工具。其次,学习能力主要可分为演绎法和归纳法。增强学习就像是基于奖赏的演绎法,给定外界环境和相应的奖赏函数,我们最终产生合法的决策出来。深度学习就像是基于经验以及记忆的归纳法,给定输入输出,然后通过神经网络来学习表征。最后关于自省能力,这也是人工智能可以产生自我意识、并独立于人类存在的关键。自省从某种程度可以从增强学习来习得,通过不断试错以及奖赏,『增强/强化』自我的决策。但这种自省又受限于其存在的世界观,就像二维线段只能盲人摸象般地观测到三维球体,而三维球体却可以完整地观测二维线段。但总之,只要定义好了世界以及奖赏,我认为相应的自省能力就是在给定环境下不断优化自己的学习能力(即一阶导数大于零)。
什么是深度增强学习
深度学习
深度学习(deep learning)是机器学习拉出的分支,它试图使用包含复杂结构或由多重非线性变换构成的多个处理层对数据进行高层抽象的算法。 – 维基百科
根据维基百科的解释,深度学习是一种利用多层非线性变换处理网络结构来进行表征学习的通用框架。 得益于计算机性能的提升,深度学习重新对人工神经网络方法进行品牌重塑。其核心解决问题是,如何用尽可能少的领域知识,给定输入 \(\boldsymbol{x}\) 和输出 \(\boldsymbol{y}\) ,来学习从输入到输出的 映射 \(\mathcal{DL}(\boldsymbol{x}, \boldsymbol{w})\) ,其中 \(\boldsymbol{w}\) 是需要优化的参数, \(\mathcal{DL}(\cdot)\) 在深度学习里由多层非线性网络结构进行表示(不同机器学习方法会有不同的刻画,比如随机森林、支持向量机等等),常见的架构方式包括深度神经网络(Deep Neural Networks),深度信念网络(Deep Belief Networks)、卷积神经网络(Convolutional Neural Networks)、递归神经网络(Recurrent/Recursice Neural Network)等等。下图直观的给出了这种逐层嵌套的网络结构,
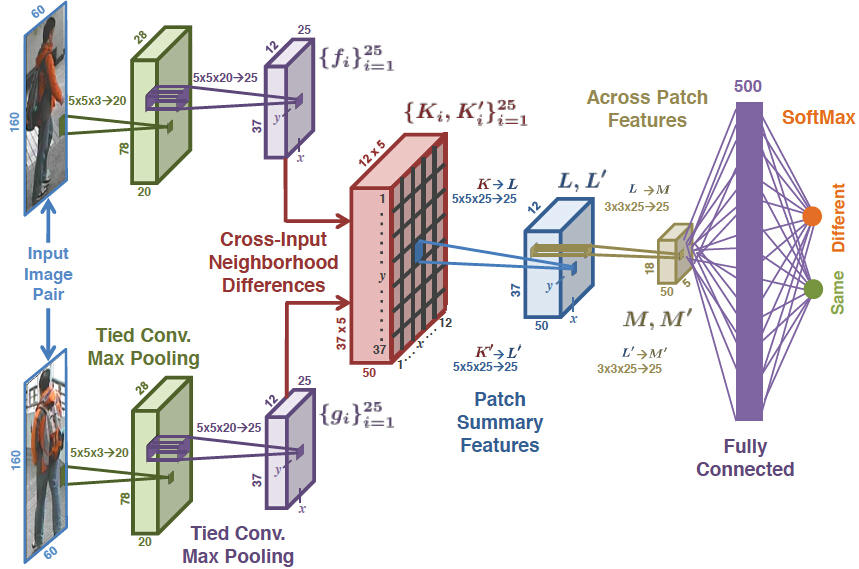
损失函数 $\mathcal{L}(\mathcal{DL}(\boldsymbol{x}, \boldsymbol{w}), \boldsymbol{y})$。这个损失函数衡量了真实和预测输出值之间的差异,常见的比如说对数损失函数、平方损失函数、指数损失函数、Hinge损失函数、各类Norm的损失函数等等2。 同时为了提高模型的泛化能力,往往需要对损失函数进行 正则化 (regularization)处理。一般需要尽量把损失函数转化为凸函数,如果函数不够光滑的话可以利用Moreau-Yoshida regularization进行处理以方便梯度的计算,最终利用 梯度下降法 来进行优化而得到 \(\boldsymbol{w}^{*} = \arg \min_{\boldsymbol{w}} \mathcal{L}(\mathcal{DL}(\boldsymbol{x}, \boldsymbol{w}), \boldsymbol{y})\) ,然后就可以利用 \(\mathcal{DL}(\boldsymbol{x}, \boldsymbol{w}^{*})\) 来进行预测了。下图展示了神经网络的一种架构,以及各个隐含层所学习到的表征,可以看到不同隐含层有不同层次的抽象学习。比如说,有的负责颜色,有的负责形状,有的负责部件等等。
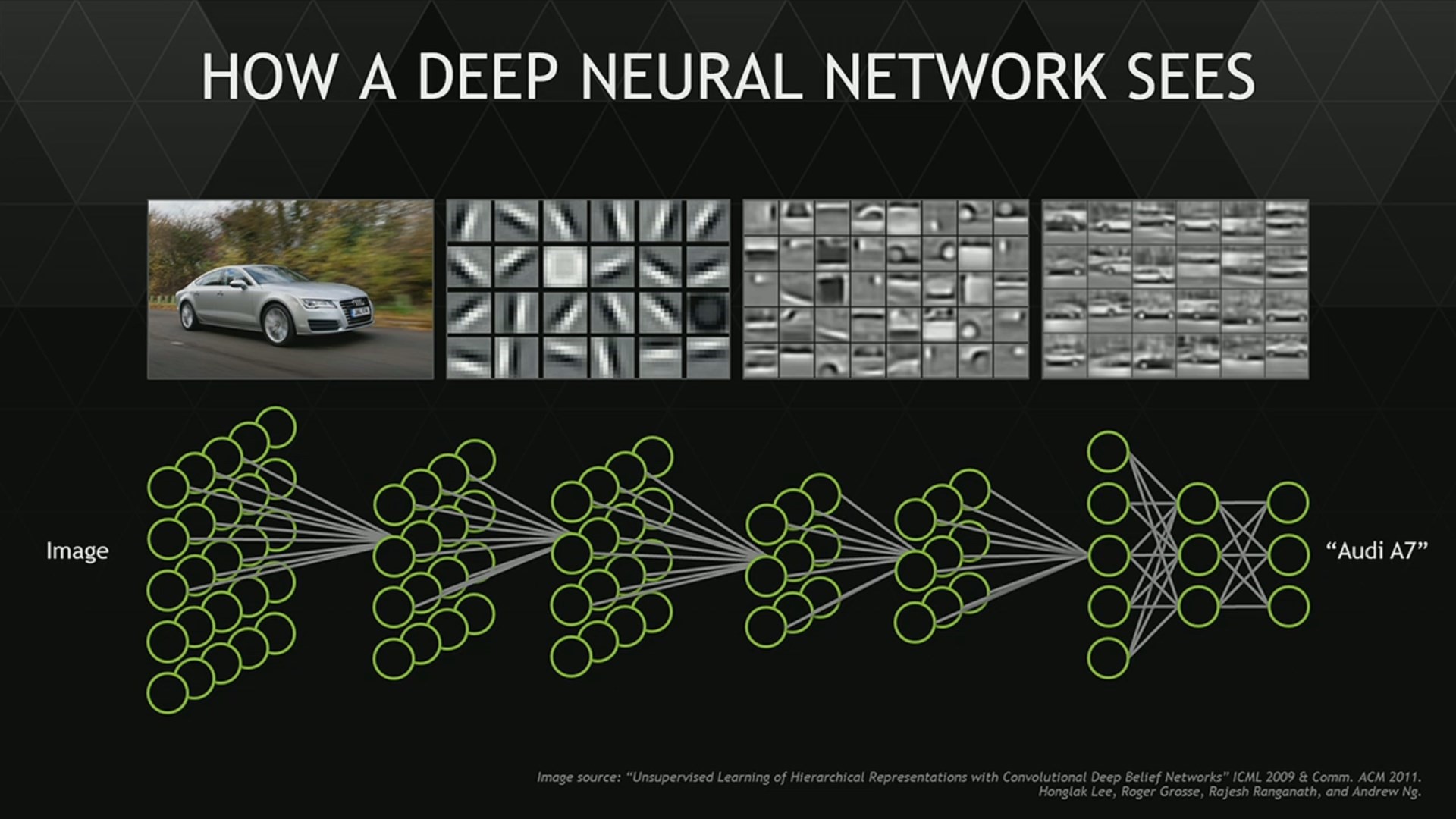
增强学习
强化/增强学习是机器学习中的一个领域,强调如何基于环境而行动,以取得最大化的预期利益。其灵感来源于心理学中的行为主义理论,即有机体如何在环境给予的奖励或惩罚的刺激下,逐步形成对刺激的预期,产生能获得最大利益的习惯性行为。这个方法具有普适性,因此在其他许多领域都有研究,例如博弈论、控制论、运筹学、信息论、仿真优化方法、多主体系统学习、群体智能、统计学以及遗传算法。 –维基百科
简而言之,增强学习是一种基于环境反馈而做决策的通用框架。 具体到机器学习领域,很多人往往知道 监督式学习 和 非监督式学习 (甚至半监督式学习),但却不知道第三类机器学习方法,即增强学习。 因为增强学习强调与环境的交互,我认为是离普遍意义上的人工智能更接近的一个领域。 这里『增强』或者『强化』的意思是,根据不断试错而得到的奖惩来不断增强对趋利决策的信念。David Silver下面这张图很好的总结了增强学习的研究主体,即 Agent 、 Environment 以及 State 。
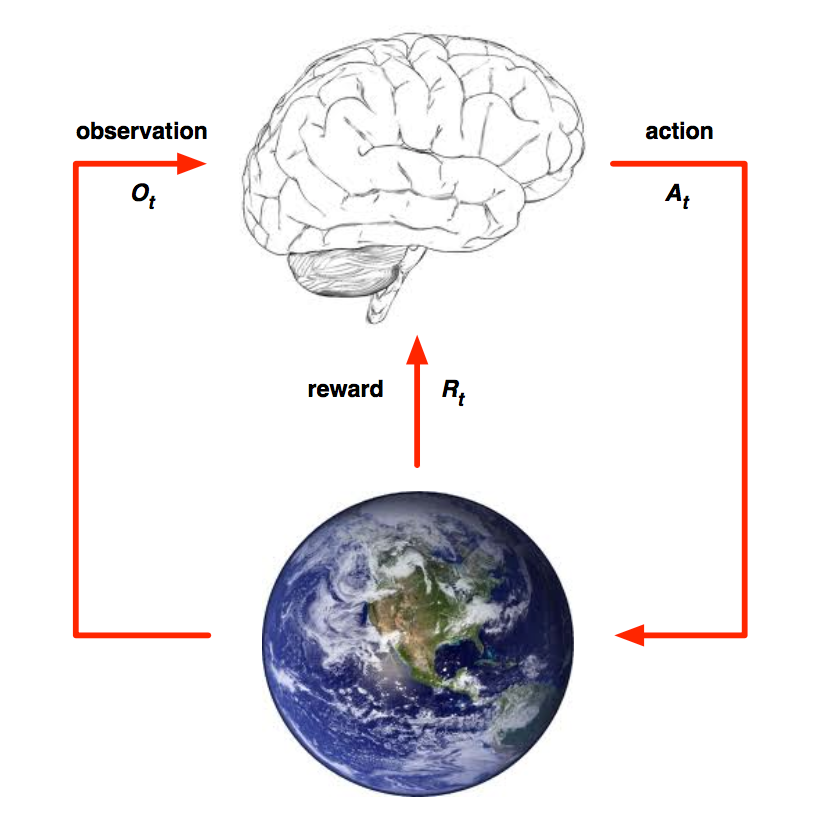
action ) \(a_{t+1}\) 。然后给定当前的状态 \(s_{t}\) 以及 Agent的决策 \(a_{t+1}\) ,Environment决定下一轮 \(t+1\) 的状态 \(s_{t+1}\) 、给Agent的报酬( reward ) \(r_{t+1}\) 、以及它可观测到的其他信息 \(o_{t+1}\) 。最后,循环往复直到任务完成。不同于Planning(规划)问题,Learning(学习)问题一开始并不知道Environment的全部情况,因此需要逐步试错学习环境以及调整自身决策。 关于奖赏的机制这里有一个假设,那就是假定所有的目标都可以被刻画为期望累积收益的最大化。 从上面的描述可以看到关于Agent,有三个很关键的组成要素,
Policy function(策略函数):从状态到决策的映射- Deterministic policy: \(\pi(s_{t}) = a_{t+1}\)
- Stochastic policy: \(\pi(s_{t}) = \mathbb{P}(a_{t+1} | s_{t})\)
Value function(价值函数):从状态以及决策到期望累积收益的映射- Bellman equation of
Q-value function: \(Q^{\pi}(s_{t}, a_{t+1}) = E^{\pi}[r_{t+1} + \gamma r_{t+2} + \gamma^{2} r_{t+3} + \dotsc | s_{t}, a_{t+1}] = E^{\pi}[r_{t+1} + \gamma Q^{\pi}(s_{t+1}, a_{t+2}) | s_{t}, a_{t+1}]\) - Bellman equation of
Optimal value function:\(V(s_{t}) = Q^{*}(s_{t}, a_{t+1}) = \max_{\pi} Q^{\pi}(s_{t}, a_{t+1}) = E^{*}[r_{t+1} + \gamma \max_{a_{t+2}} Q^{*}(s_{t+1}, a_{t+2}) | s_{t}, a_{t+1}]\)
- Bellman equation of
Model function(环境函数):从状态以及决策到环境决策的映射3- Deterministic environment: \(e(s_{t}, a_{t+1}) = [s_{t+1}, r_{t+1}, o_{t+1}]\)
- Stochastic environment: \(e(s_{t}, a_{t+1}) = \mathbb{P}([s_{t+1}, r_{t+1}, o_{t+1}] | s_{t}, a_{t+1})\)
通过折现因子 \(\gamma\) 的引入,Q-value function一来可以转化为贝尔曼方程并满足无后效性以及最优子结构的特征;并且多期的折现又比单纯的one-step lookahead贪婪策略更加具有远见。 总而言之,求解增强学习问题的核心实际上在于价值函数的贝尔曼方程,这也是动态规划里标准的状态转移方程,即定义好边界以及该方程后,就可以通过倒推法或者带记忆的递归予以解决。 不过增强学习也可以通过直接搜索最优策略或者学习环境的奖惩套路来解决。 实际上,这三个要素正是强化学习同深度学习结合的关键。 正如David Silver所说 4,
Reinforcement Learning defines the objective. Deep Learning gives the mechanism. – David Silver
二者的融合
对于复杂的任务以及环境而言,Q-value function实际上很难穷举的完的(针对每一个状态和决策都要给一个累积期望收益值),因此一般需要通过历史信息来估计这一函数。同样的,对Policy function和Model function也有类似的情况。 所以在给定增强学习三大求解目标(Policy-based, Value-based, Model-based)之后,我们便可以利用深度学习来利用历史输入输出来估计这三大目标函数。
怎么利用深度增强学习解决问题
正如上文的分析,David Silver将深度增强学习算法分为如下三大类5。 下文将先从增强学习的角度分析如何做决策,然后从深度学习的角度来分析如何学习相应的策略函数、估值函数以及环境函数。
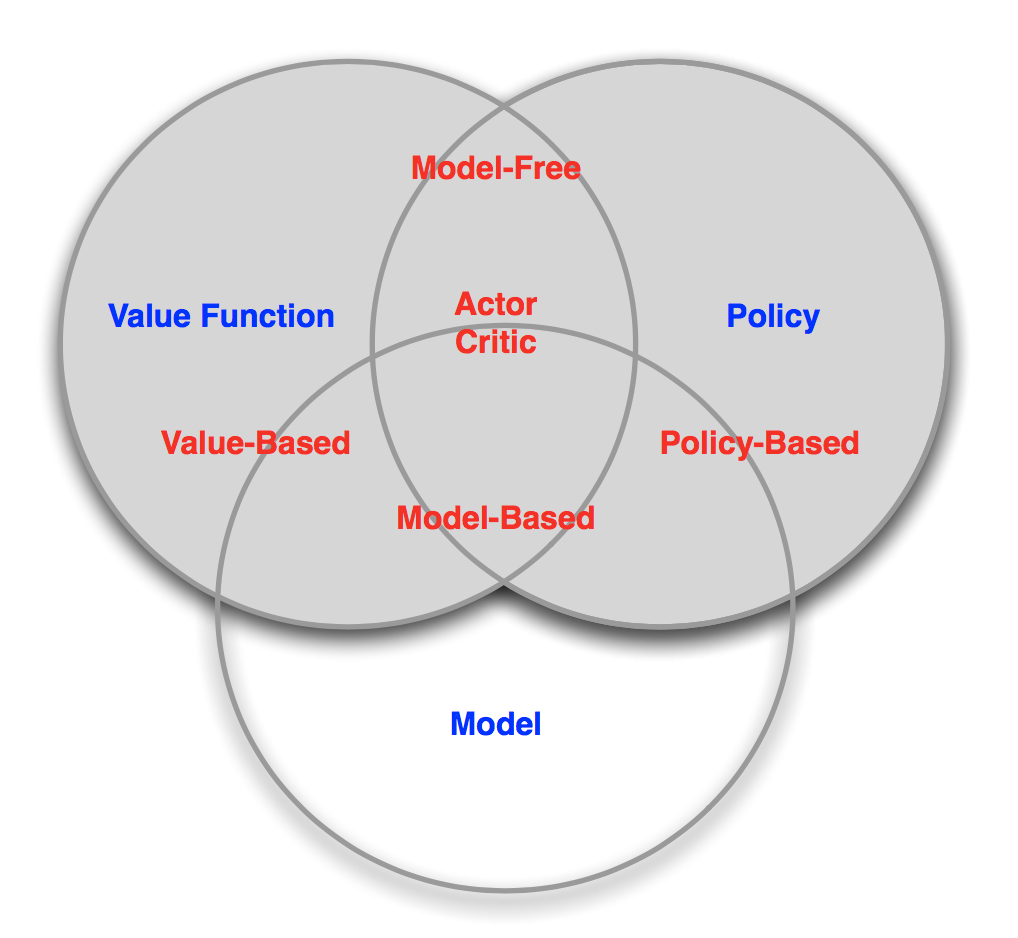
Policy-based DRL
下图展示了利用 Policy Iteration Algorithm 来解决增强学习问题的思路。即给定任意初始策略 \(\pi_{0}(s)\) ,然后利用估值函数 \(V_{0}(s)\) 对其评价,基于该估值函数对策略进一步优化得到 \(\pi_{1}(s)\) 。循环这一过程,直至策略达到最优而不能进一步改善。

至于在深度学习方面,首先对policy function进行参数化 $a = π(s, \boldsymbol{u})$,其中 \(\boldsymbol{u}\) 为神经网络的参数。其次,参数化后的累积期望收益函数为 \(V(\boldsymbol{u}) = E[r_{1} + \gamma r_{2} + \gamma^{2} r_{3} + \dotsc | \pi(\cdot, \boldsymbol{u})]\) 。然后,我们就可以得到 策略梯度 (Policy Gradients),在随机性策略函数下为 \(\frac{\partial V(\boldsymbol{u})}{\partial \boldsymbol{u}} = E[\frac{\partial log \pi (a | s, \boldsymbol{u})}{\partial \boldsymbol{u}} Q^{\pi}(s, a)]\) ,而在确定性策略函数下为 \(\frac{\partial V(\boldsymbol{u})}{\partial \boldsymbol{u}} = E[\frac{\partial Q^{\pi}(s, a)}{\partial a} \frac{\partial a}{\partial \boldsymbol{u}}]\) 。最后,便可以利用梯度下降算法来寻找最优的神经网络参数 \(\boldsymbol{u}\) 6 。
Value-based DRL
下图是解决增强学习问题的 Value Iteration Algorithm 的伪代码。即给定任意初始估值函数 \(V(s)\) ,利用贝尔曼方程递推得逼近真实的估值函数。至于这种方法的收敛速度以及是否收敛,我还不是太清楚,需要日后再做总结。

至于深度学习方面,类似的,先对value function进行参数化 \(Q(s, a, \boldsymbol{w}) \approx Q^{*}(s, a)\) ,那我们的目的就是找 \(\boldsymbol{w}\) 。然后,就是优化损失函数 \(L = (r + \gamma \max_{a} Q(s^{'}, a^{'}, \boldsymbol{w}) - Q(s, a, \boldsymbol{w}))^{2}\) 7。David Silver在这里提到如果样本之间存在相关性或者收益函数非平稳,容易导致价值函数的不收敛,因此需要一些机制来予以解决。
Model-based DRL
关于Model-based DRL,David Silver讲的比较少,主要举了Alpha Go的例子,即我们完美知道环境的信息(走子规则、胜负规则等等)。大致意思还是利用神经网络来代替真实的环境函数,也就是让Agent有能力预测环境下一期的状态以及收益等等,基于此来优化Agent的决策过程。下图是网上8 找到的 Model Iteration Algorithm 的伪代码,基本就是通过对状态转移函数以及奖惩函数的搜索,来估计价值函数。

深度增强学习有哪些用途
可以看到凡是任务导向型,并且目标可以被奖惩函数刻画的,均可以利用深度增强学习来解决,所以其应用范围还是蛮广的。 以下举了深度增强学习的若干应用,视频均来自Youtube,因此需要科学上网。
游戏策略
机器人控制
无人驾驶
探索环境
学会走路
结语
如果说达尔文的进化论是人类关于自身起源的一次冲击,那么通用型人工智能的诞生便是对人类未来的另一次冲击。 在Alpha Go之前,人们认为人工智能战胜人类围棋高手大概还需要十多年的样子,然而技术的发展速度实在是不可想想。让我们扩大时间的尺度,想想十年前、百年前、千年前中国的样子,在看看我们现在的生活,不能说是天翻地覆,但显然得益于技术的发展,我们的生活有了更多的便捷。 也不禁畅想未来,说不定下个技术引爆点没有想象中的那么远,或许明年或许明天。 所以,对于大多数人而言,还是有必要提前接触这些前沿的领域,一来不至于自己到了未来成为新『文盲』,二来也不会沦落到被高新技术革了命。
关于【深度增强学习】系列的说明
延伸阅读
- 公开课
- 基础介绍
- 书籍
- 论文
- 资源列表
- 其他
Footnotes:
详见知乎Live:深入浅出说围棋人工智能
各类损失函数的定义及应用具体请见http://www.csuldw.com/2016/03/26/2016-03-26-loss-function/
在David Silver的Tutorial里并没有详细讲Model函数的刻画,这里的映射仅仅是我自己的理解,即通过model来作为刻画环境的媒介
这个大概就是Deep Policy Networks(DPN)的大致思路
这个大概就是Deep Q-Networks(DQN)的大致思路
 本作品采用知识共享署名 2.5 中国大陆许可协议进行许可。欢迎转载,但请注明来自Mount Greenwicher的文章《深度增强学习【1】走向通用人工智能之路》,并保持转载后文章内容的完整与无歧义。本人保留所有版权相关权利。
本作品采用知识共享署名 2.5 中国大陆许可协议进行许可。欢迎转载,但请注明来自Mount Greenwicher的文章《深度增强学习【1】走向通用人工智能之路》,并保持转载后文章内容的完整与无歧义。本人保留所有版权相关权利。