Codeforces - 598D Igor In the Museum

Codeforces - 598D Igor In the Museum 解题报告，带记忆的深度优先搜索

前文曾提到过解决一个算法问题，大概可以划分为三个阶段。第一阶段是算法设计，即人脑准确无误理解算法问题，并设计算法，这一阶段属于模型在思维上的构建。第二阶段是算法实施，即程序员用自己钟爱的语言对思维上的模型进行现实化，依靠计算机来获得结果，这一阶段属于模型在代码上的构建。最后一阶段，即计算机执行程序员给定的命令，并返回其所希望的结果，这一阶段属于模型在计算机硬件上的构建。为了保证最终输出的正确性，这三个阶段不能发生任何可预见或者意想不到的错误。算法运行中的精度问题在前文中已有所描述，这一次我们来谈谈算法实施阶段，并以Codeforces 598D来说明如何写更精简的代码。

问题描述

cf598d.jpg

这道题的基本意思是说，给定一个博物馆二维平面空间布置，其中 . 表示通道， * 表示一堵墙，每一堵墙的两面都挂着画。然后问给定Igor的起始位置，他最多能够观赏多少副画。

初步思考

分析

Igor只能在连通的通道里移动，因此问最多能够观赏多少幅画，那么首先先确定Igor可移动的连通区域，然后确定其边界，最后对每个边界，确定可看到的画作的数目再加和即可。确定连通空间的范围可以转化成深度优先搜索，既以当前位置为搜索树的根节点，然后其上下左右连接点为四个子节点。若子节点为墙，则搜索完毕；若子节点为已搜索过的通道，则毋需再次搜索；若子节点为通道且未搜索，那么利用同样的法则递归的搜索。

代码

由此，我们可以得到如下的算法。

 1: #%% Version 1: given (x,y) search valide empty regions and calculate max_pic_num
 2: #Search irreducible valid regions recurisvely
 3: #!!no need to return any value for this recurisve function
 4: def searchPicLayout(m,x,y):
 5:     global pic
 6:     global visit
 7:     #visit (x,y)
 8:     visit.add((x,y))
 9:     #valid direction
10:     move = [(0,-1),(1,0),(0,1),(-1,0)]
11:     for i in range(len(move)):
12: 	#find neighbot (ith direction)
13: 	d = move[i]
14: 	nx,ny = x+d[0],y+d[1]
15: 	#check neighbor
16: 	if m[nx][ny] != '*':
17: 	    #check key of (nx,ny) in explore
18: 	    if not((nx,ny) in visit):
19: 		#explore new valid unvisited point
20: 		searchPicLayout(m,nx,ny)
21: 	else:
22: 	    #impassable point and mark the picture
23: 	    pic[nx][ny] += 1
24: #Read Input
25: I = lambda:map(int,input().split())
26: n,m,k = I()
27: museum = []
28: for _ in range(n):
29:     museum.append(input())
30: #Output
31: for _ in range(k):
32:     x,y = I()
33:     #records layout of pictures, 1 represents picture exists
34:     pic = [[0 for j in range(m)] for i in range(n)]
35:     #records visited points
36:     visit = set()
37:     #find the pictures can be viewed
38:     searchPicLayout(museum,x-1,y-1)
39:     #Output best solutions
40:     print(sum([sum(r) for r in pic]))

然而，这段代码并没有通过Codeforces的测试，在第10号测试数据上超时了。那么有什么可以优化的地方么？

生成缓存

分析

注意到这道题的测试数据里每一次都要计算若干起始点下最多可看到的画作数量，因此有可能出现某些起始点实际上归属于同一个连通区域。而先前的算法针对每一个新的起始点，都进行新的计算，因而可能会出现大量的重复计算。因此，我们可以有如下的第一个算法优化思路，即进行缓存，

优化1：标记已解决的起始点及其连通点的最优值，进行缓存记录。

代码

相应的代码如下所示

 1: #%% Version 4: based on Version 1, but make indexing for already retrieved information
 2: #Search irreducible valid regions recurisvely for (x,y)
 3: #!!no need to return any value for this recurisve function
 4: def searchRegion(m,x,y):
 5:     global visit
 6:     #visit (x,y)
 7:     visit.add((x,y))
 8:     #valid direction
 9:     move = [(0,-1),(1,0),(0,1),(-1,0)]
10:     for i in range(len(move)):
11: 	#find neighbot (ith direction)
12: 	d = move[i]
13: 	nx,ny = x+d[0],y+d[1]
14: 	#check neighbor
15: 	if m[nx][ny] == '.' and not((nx,ny) in visit):
16: 	    searchRegion(m,nx,ny)
17: 
18: #Read Input
19: I = lambda:map(int,input().split())
20: n,m,k = I()
21: museum = []
22: for _ in range(n):
23:     museum.append(input())
24: #Indexing
25: ans = [] #max_pic_num for each region
26: region = [[-1 for j in range(m)] for i in range(n)] # region id for each point
27: region_id = -1
28: for _ in range(k):
29:     x,y = I()
30:     #check wheter region including (x,y) is explored
31:     if region[x-1][y-1] == -1:
32: 	#new region
33: 	region_id += 1
34: 	#records visited points
35: 	visit = set()
36: 	#searching valid regions
37: 	searchRegion(museum,x-1,y-1)
38: 	#update region id and calculate max_pic_num
39: 	max_pic_num = 0
40: 	for p in visit:
41: 	    a,b = p[0],p[1] #cannot use x,y as var_name
42: 	    region[a][b] = region_id
43: 	    max_pic_num += [museum[a][b-1],museum[a+1][b],museum[a][b+1],museum[a-1][b]].count('*')
44: 	#update ans
45: 	ans.append(max_pic_num)
46:     print(ans[region[x-1][y-1]])

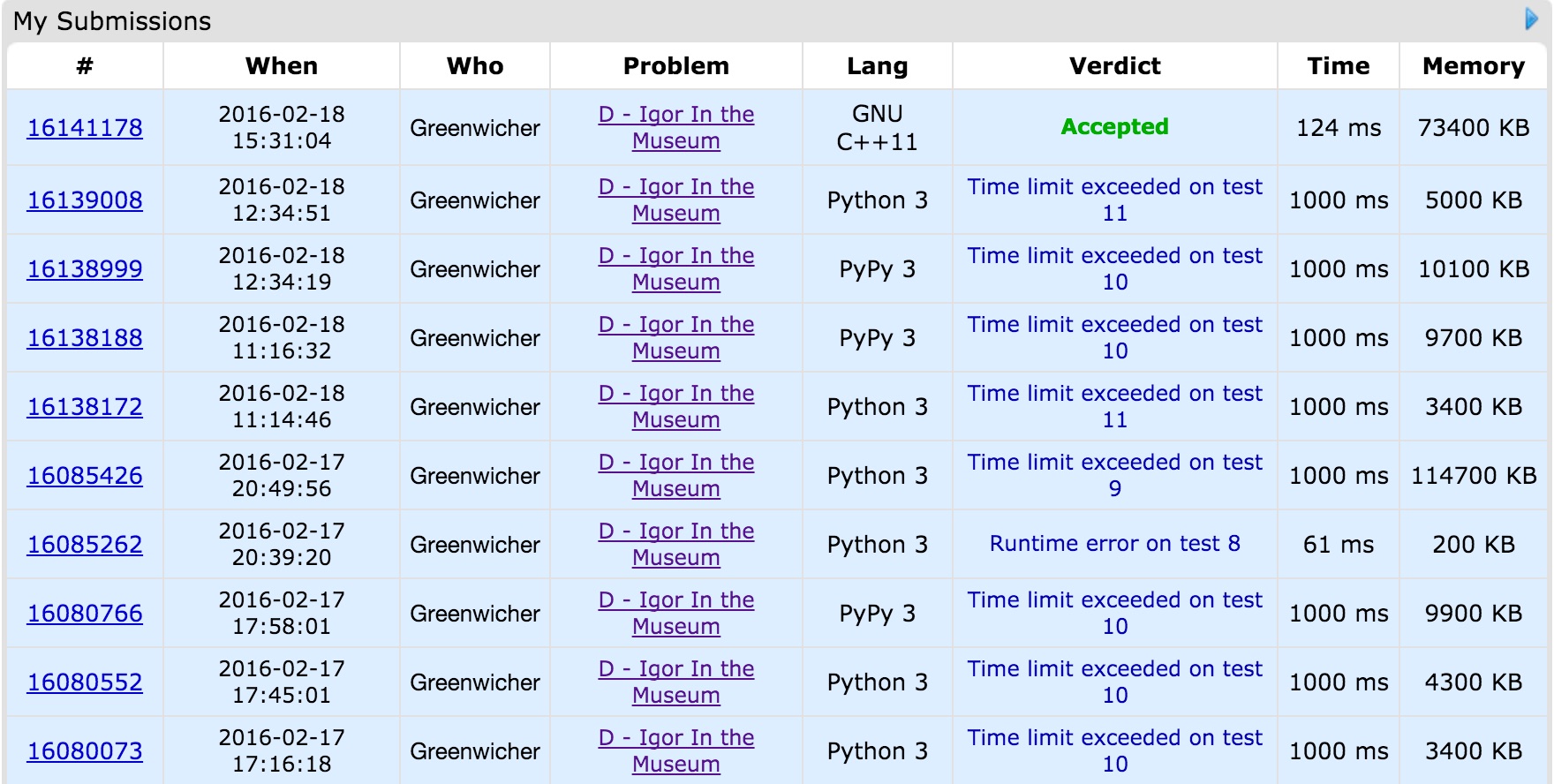
然而即使这样操作了，这段算法还是卡在了第11号测试数据上（后来发现是 Python3 的效率缘故，换做 C++ 后，一次AC）。

ac.jpg

全方位的深度优先搜索

分析

回到正题，那么这道题对我们算法实施有什么借鉴意义呢？回想前面的分析，我们主要有两个想法

通过深度优先搜索确定连通区域，然后确定边界，并计算可观赏到的画作数量。
解决一个初始点问题，便同时解决了以该连通区域其他点为初始点的问题。因此对已解决的初始点问题的连通区域也进行缓存标记。

也就是说我们程序的输出有两个，一是可观赏到的最多画作数量，二是起始点的连通区域。那么能否再进行深度优先搜索的同时，兼顾这两个任务，以减少代码数量呢？前述算法在进行深度优先搜索时，仅仅把递归函数当做一个过程，而并无返回值。实际上，当我们搜索到一个节点为墙时，即意味着我们看到了一副画，返回1；如果搜索到通道节点时，那么什么也没看到，返回0。同时，再搜索的过程，我们便可以标记出这些连通点的区域代号。这给了我们第二个算法优化思路，

优化2：深度优先搜索的同时，记录连通区域以及已看到的画作数量

代码

相应的代码如下

 1: #%% Version 5: inspired by 14440455
 2: #retrieve region i which includes cell (x,y) and
 3: #return the max_pic_num and mark the region id for each cell
 4: def search(x,y,i):
 5:     global region
 6:     #impassable cell
 7:     if museum[x][y] == '*': return 1
 8:     #already visited
 9:     if region[x][y] != -1: return 0
10:     #mark region id
11:     region[x][y] = i
12:     #explore recursively (dfs)
13:     return search(x,y-1,i)+search(x+1,y,i)+search(x,y+1,i)+search(x-1,y,i)
14: #Input
15: I = lambda:map(int,input().split())
16: n,m,k = I()
17: museum = []
18: for _ in range(n):
19:     museum.append(input())
20: #Processing
21: ans = [0 for i in range(n*m)] #max_pic_num for some input cell
22: region = [[-1 for j in range(m)] for i in range(n)] #region id for each point
23: for i in range(k):
24:     x,y = I()
25:     #unexplored
26:     if region[x-1][y-1] == -1:
27: 	ans[i] = search(x-1,y-1,i)
28:     #Output
29:     print(ans[region[x-1][y-1]])

最终通过测试的是如下 C++ 代码，

 1: //version 1
 2: #include<cstdio>
 3: #include<iostream>
 4: #include<vector>
 5: using namespace std;
 6: int n,m,k;
 7: char museum[1001][1001];
 8: int region[1001][1001];
 9: int search(int x, int y, int i)
10: {
11:   if (museum[x][y]=='*') return 1;
12:   if (region[x][y]) return 0;
13:   region[x][y] = i;
14:   return search(x,y-1,i)+search(x,y+1,i)+search(x-1,y,i)+search(x+1,y,i);
15: }
16: 
17: int main()
18: {
19:   cin>>n>>m>>k;
20:   int region_id=0;
21:   vector<int> ans;
22:   ans.push_back(0);
23:   for(int i=1;i<=n;i++) scanf("%s", museum[i]+1);
24:   for(int i=0;i<k;++i){
25:     int x,y;
26:     scanf("%d%d",&x,&y);
27:     if (!region[x][y]){
28: 	region_id++;
29: 	ans.push_back(search(x,y,region_id));
30:     }
31:     printf("%d\n",ans[region[x][y]]);
32:   }
33: }

代码量是不是比之前要少多了啊~

反思

本题目其实就是深度优先搜索的变种，并且给了我如下两个经验。

如果日后有需要解决类似问题的需求，那么最好现在做缓存，以减少日后的重复计算。【恰逢AlphaGo 3：0获胜人机大战，值得一提的是这次AlphaGo的大量自我对弈以及棋谱学习，其实也是一种缓存】
更高效的利用过程主导的递归函数来更新所需要的输出值

本作品采用知识共享署名 2.5 中国大陆许可协议进行许可。欢迎转载，但请注明来自Mount Greenwicher的文章《Codeforces - 598D Igor In the Museum》，并保持转载后文章内容的完整与无歧义。本人保留所有版权相关权利。

据说爱打赏的人运气都不会差

微信打赏

支付宝打赏

留言

新大陆被发现了次！